[教學活動]三隻小蛛 Xpiders（搭配單元：一上 一元一次方程式）

這幾年在一次方程式的教學經驗中，
我察覺等量公理不是孩子們遇到最關鍵的難題，
而是不懂式子的意義及各數間的影響關係及順序。
例如在式子(5+2x)/3中，
有5有2有3，從x變為(5+2x)/3時，其運算順序為「乘以2」-「加5」-「除以3」，
但課本並未過多著墨在這概念上。
因此在這一屆國一新生的一元一次方程式單元中，

我想花點心思讓孩子能瞭解式子的意思，
所以在暑假前就設計了「x超人變身術」這張學習單。

前幾堂課做了一些練習後，
今天突發奇想，讓孩子來畫畫蜘蛛吧！
如果你問我為什麼要畫蜘蛛，我的回答是單純想增加一點趣味。
Why so serious？

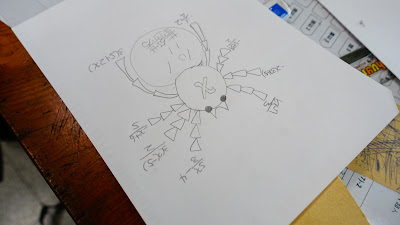
我的草稿及題目，
目標是將腳的末稍式子經過三個步驟變為x。
所以箭頭是往身體部分畫的。

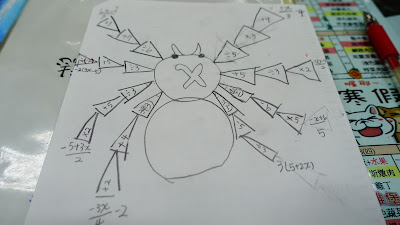
每道題目都是三步驟還原為x。

第二組題目。

原來要畫三隻蜘蛛的，後來就畫了一隻烏賊。
（我知道烏賊不是八隻腳，有跟孩子們強調）

下面是孩子們畫的蜘蛛，還有許多不錯的創意展現，

但是我一個一個人檢核，忙到沒時間拍照記錄。

 

國中生一定要會的1000道基本題（4/10 第301-400題答案）

留言前請先詳閱文章

留言前請先詳閱文章

留言前請先詳閱文章

題目單下載及各百題答案連結請至：

國中生一定要會的1000道基本題（1/10 主篇及前100題答案）

D140 301-305

D139 306-310

D138 311-315

D137 316-320

D136 321-325

325題的答案有誤

D135 326-330

D134 331-335

D133 336-340

D132 341-345

D131 346-350

第349題改為4:25

D130 351-355

D129 356-360

D128 361-365

D127 366-370

D126 371-375

D125 376-380

D124 381-385

D123 386-390

D122 391-395

D121 396-400

[教學活動]一分鐘挑戰（搭配單元：三上 幾何與證明）

這次的證明單元，先以證明接龍作為開頭。

孩子們的邏輯及數學基礎都不佳，
所以花了兩節課的時間，
許多孩子仍然不大能分辨相鄰句子的因果關係。

所以接續的是讓孩子動手獨力書寫，
將12題依易難順序編號，
採試題切割分段法的方式，讓孩子一題一題寫，
讓我確認無誤後才可以領取下一題。

然而，即使孩子寫完了整題，
他們還是似懂非懂，沒辦法百分之百瞭解前因後果。

例如在下圖所示的題目中，
推理過程的最後三句敘述是：
「兩個三角形相似」，「角A=角C」，「線段AB與線段CD互相平行」。

其中「兩個三角形相似」是「角A=角C」的因

（因為兩三角形相似，所以其對應角相等），
而「角A=角C」搖身一變變成「線段AB與線段CD互相平行」的因

（因為內錯角相等，所以平行）。
雖是短短的三句話，卻包含了不少關鍵概念。
我一句「為什麼角A會等於角C」時，
他們的回答通常就是「內錯角」，
而這種「倒因為果」或是「缺少充足理由」的狀況，
是在經過好多好多堂課的訓練之後仍會頻繁出現的錯誤。

喔~這好難！

一題，需要多少時間才能教會所有孩子呢？

「寫下來的，不一定是會的。」
我有了這個想法後，決定讓孩子來「說說」課本最後兩個例題：
「三角形兩對角線中點連線性質」以及「內分比性質」。

不用詳細的說明線段或圖形的名字

（例：說到三角形ABF只需要用手比給我或圈給我看就可以），
但限制要在一分鐘內講完整個過程（我使用一分鐘沙漏來計時）。

限制一分鐘的好處在於節省大家排隊的時間，
也強迫孩子必須非常清楚知道每句他說的話，
而不是寫下連自己都看不懂的東西。

下面影片是一位孩子試著講解的過程，
錄下的這一次他並沒有成功。

但經過多次的挑戰後完成一分鐘挑戰。

在這一題的說明中，
孩子很輕易可以說明三角形全等的原因，
卻都沒辦法接著說出全等是為了得到什麼，
也往往會忘記說明為什麼線段EF會與兩底互相平行。
所以很多人被我退回了五六次以上。

最終花了兩節課的時間，
還是沒有辦法讓全班完成兩則證明的一分鐘挑戰。

要是孩子花了兩節課都沒辦法弄懂一件事情的始末，
我在臺上講得再清楚，應該都是事倍而無功吧！？

如果我有時間，我好希望讓每個孩子弄懂並說給我聽，
並在過程中接受我的質問與挑戰。
但，終究還是這個但。
一題證明題花了我兩節課仍未讓全部人通過一分鐘挑戰，
我還是得在進度的威脅下妥協，繼續前行。

經過這一次的挑戰後，
我更認為我要盡量減少在臺上說話的時間，
也更佩服能讓孩子上臺發表的教師夥伴，
因為，孩子能夠順暢的說出數學，
數學及表達能力都不是短時間可以培養起來的。